今天來講講眾所皆知、經典到不能再經典的、除了陣列以外的線性資料結構代表：堆疊和佇列。
堆疊 (Stack) 是一種先進後出的資料結構，它支援 push() 和 pop()。佇列 (Queue) 是另一種先進先出的資料結構。有趣的問題如下：我們能不能利用一些堆疊來模擬佇列呢？

當然可以：讓我們考慮以下「用兩個 stack 模擬一個 queue」的演算法。

假設我們有兩個堆疊 S1 和 S2。

• push(x):
  • 把 x 放到 S1 上面。
• pop():
  • 查看 S2，如果 S2 是空的，那我們就把所有 S1 的東西依序拿出來，然後放進 S2 裡面。因為被倒過來兩次了，所以現在 S2 裡面的東西就是按照放進來的順序排著。

分析也很簡單：由於每一個元素被放進 S1、S2 各一次，然後就被拿走了，因此進行 n 個操作後的時間複雜度是 O(n)，均攤起來每一個操作的時間複雜度是 O(1)，心滿意足。

真的心滿意足嗎？想像一下，如果今天在連續 100000 次 push() 之後，突然來一個 pop()，我們得花 199999 個操作才能把埋藏在 S1 底下的第一個東西拿出來耶。雖然平均起來每一個操作只花了O(1)時間，但這個單一的操作未免也太久了吧！

這個就是均攤分析與最差情形分析的差別。上述的演算法在最差情形下，某一步可能仍會達到 \Theta(m) 時間複雜度，其中 m 指的是從頭開始到目前為止的操作總數。要如何作到避免某個元素被深埋在 珊瑚海 堆疊底下呢？如果我們的目標是作到最差情形也要 O(1) 之內完成 push 或 pop 操作的話，勢必要在 push 新東西、或 pop 已經準備好的舊東西時，偷偷先準備一些未來可能會用到的操作。而把一個從均攤分析觀點來看，還不錯的演算法，改良成最差情形分析也不錯的演算法，這樣的過程我們稱之為去均攤化（Deamortization）。

佇列模擬問題的去均攤化

兩個堆疊看來是無法阻止上面這種情形發生了。兩個堆疊不夠怎麼辦？你有沒有考慮用更多的堆疊呀～讓我們來看看下面這個實作方法。

用九個堆疊實作佇列

這裡的技巧是，偶爾會有某個元素同時留在兩個堆疊裡面。這麼一來，我們就可以用某種「交叉掩護前進」的方式每一次更新一點點堆疊。圖片解釋如下：

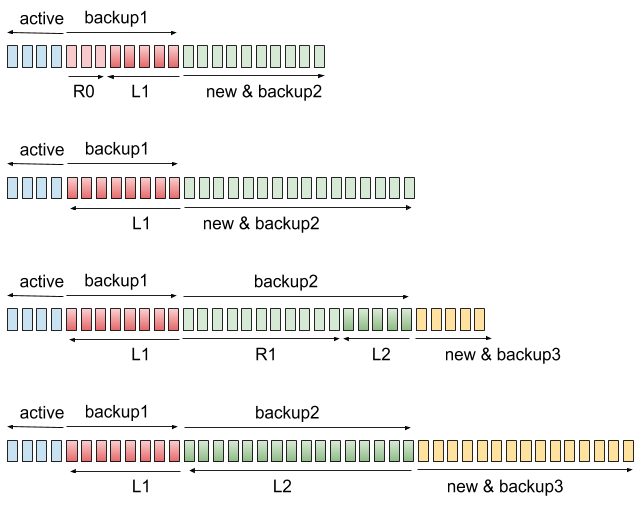
接下來就可以把 backup1 與 L2 接在一起，不用另起爐灶。但我們會需要同時往兩個方向長（這邊我們會需要 9 個堆疊...）。

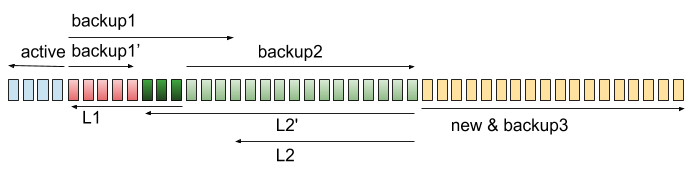
最終我們可以把 L1 跟 backup2 丟掉，就可以繼續往右邊長了！

在過程中我們總是維持 |active|+|L1|+|L2| >= 2(|R0|+|R1|+|new|)，這樣就可以保證每一次操作都是 O(1) 了！

備註

原本 stackoverflow 連結好像壞掉了...上面寫的是說可以用六個堆疊實作，但我怎麼想就是想不出來...所以只好先想出九個堆疊的方法。如果有想到六個堆疊的實作方式再麻煩留言或寄信我說喔～謝謝！

參考資料：

• https://stackoverflow.com/questions/5538192/how-to-implement-a-queue-with-three-stacks
• https://www.westpoint.edu/eecs/SiteAssets/SitePages/Faculty%20Publication%20Documents/Okasaki/jfp95queue.pdf